スミスチャート：その歴史とRF設計者にとって重要である理由

RF設計で2つの部品（たとえば電圧制御発振器（VCO）とミキサ）の間を直接接続しようとする初心者は必ず、部品のデータシートで奇妙な円形のグラフに出くわします。具体的には、Maxim Integratedが提供する500～2500MHzのVCOバッファアンプMAX2472のこのようなグラフです（図1）。これらはスミスチャートと呼ばれますが、明らかに代数や統計学の授業で見たようなグラフとは大きく異なっています。

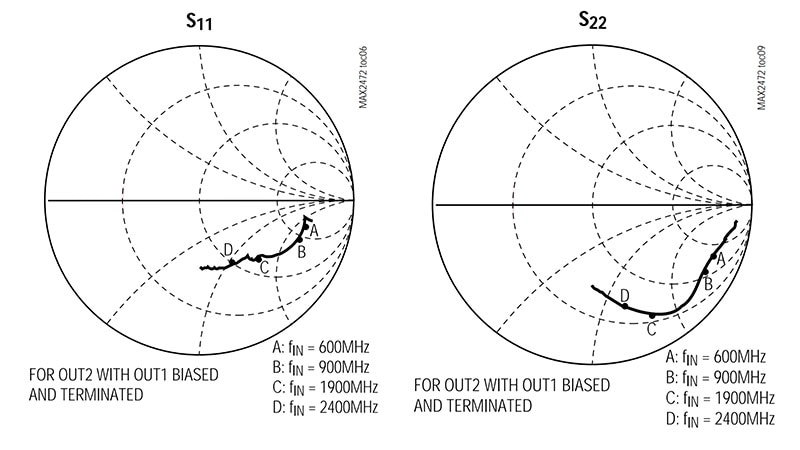図1：多くのRF部品のデータシートには、各動作周波数に対する主要パラメータの値を示すスミスチャートが記載されています。これらは、Maximが提供するVCOバッファアンプMAX2472の600、900、1900、2400MHzに対するものです。（画像提供：Maxim Integrated）。

このグラフの名称は、ベル電話研究所の技術者フィリップ・スミスにちなんでいます。彼は、伝送路および、当時は「高周波」と見なされていた最大1MHz（当時の単位名は「メガサイクル毎秒」）の定在波を理解することに取り組んでいた1936～1939年の間にこのグラフを考案し、それを改良しました。この奇妙な見た目の円形グラフは、高周波回路を対象として入出力インピーダンスに関する最適化を行う上で最も役に立ち、代わるもののないツールとなりました。強力なコンピュータとコンピュータ支援用設計（CAD）ツールの時代である現代にあっても、このことは変わりません。

スミスチャートには多くの使い方がありますが、多くの回路、特にRF設計においてきわめて重要な考慮事項として、段間の電源インピーダンスと負荷インピーダンスの整合を取る場合に、設計選択肢を効率よく視覚化する手段となります。そのような整合がきわめて重要である理由には、以下の2つがあります。

・第1に、電源から負荷に最大電力を伝送するには、電源の複素インピーダンスR_S + jX_Sが、負荷インピーダンスの複素共役であるR_L - jX_Lと等しくなければなりません。

ここで、Rはインピーダンスの抵抗成分（実部）であり、Xは（誘導性または容量性）リアクティブ成分です（図2）。

図2：RFおよび伝送路の設計における重要な課題は、電源のインピーダンスの複素共役である負荷インピーダンスを、その負荷インピーダンスが存在しない場合でも、電源から「見える」ようにすることです。（画像提供： HandsOnRF.com）

• 第2に、そのような電力損失が重要でない場合であっても（実際はほとんどの場合に重要だが）、負荷から電源へのエネルギーの反射は電源の出力回路に損傷を与える恐れがあり、それを最小化するためにインピーダンス整合が必要です。

スミスチャートが示すもの

スミスチャートは、複素反射係数（ガンマとも呼ばれ、Γの記号で表される）の極座標図です。これは、当初ほとんど不可能にも思えるような表示を実現したもので、複素インピーダンスの実部および虚部（実部Rが取り得る値の範囲は0から無限大（∞）、虚部Xはマイナス無限大からプラス無限大）を同時にグラフ化し、すべてが1枚の紙の上で完結します。

定抵抗を表す円と定リアクタンスを表す弧からなる単純化されたスミスチャートが、スミスチャートの仕組みを理解するのに良い出発点となります（図3）。追加の利点として、このグラフは散乱パラメータ（sパラメータ）と、その値が実際のハードウェア測定値および考慮事項とどう関係するかも示しています。

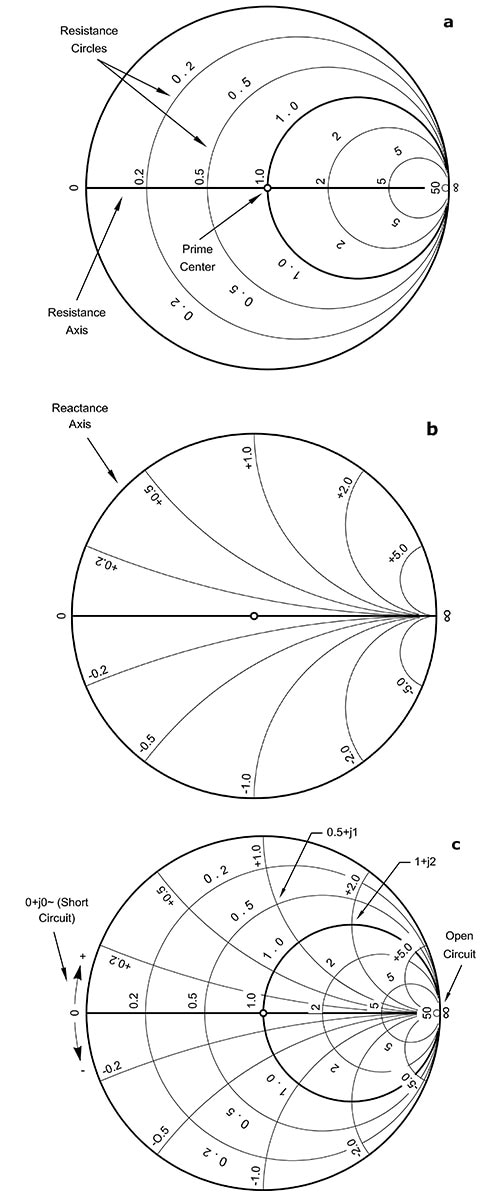図3：スミスチャートは定抵抗の円（a）と定リアクタンスの弧（b）を示しており、それらを合わせ、重ねて描くことで（c）、考えられるすべてのインピーダンスを把握できます。（画像提供： ARRL.org）

これらの複素インピーダンスの値をスミスチャートに記すと、それを使うことで、RF信号の経路または伝送路における以下のような状況を理解する上で不可欠な多くのパラメータを同定できます。

• 複素電圧および複素電流の反射係数
• 複素電圧および複素電流の透過係数
• 電力の反射係数および透過係数
• 反射損失
• リターンロス
• 定在波の損失率
• 最大電圧、最小電圧、最大電流、最小電流、および定在波比（SWR）
• 電圧および電流の定在波における形状、位置、位相分布

しかしこれは、スミスチャートの威力の一部に過ぎません。上記のパラメータを知ることは、設計者の役に立ち、しばしば必要なのですが、それと同時に、スミスチャートは以下のような解析および設計上の決定を行うためのガイドにもなります。

• 複素インピーダンスと周波数の関係の表示
• ネットワークのsパラメータと周波数の関係の表示
• 開スタブおよび短絡スタブの入力リアクタンスまたはサセプタンスの評価
• 伝送路のインピーダンスに対するシャントおよび直列インピーダンスの影響の評価
• 共振スタブおよび反共振スタブの入力インピーダンス特性（帯域幅およびQ値など）の表示と評価
• 単一または複数の開スタブまたは短絡スタブ、4分の1波長線路セクション、集中定数LCコンポーネントを使用したインピーダンス整合ネットワークの設計

スミスチャートの利点

詳細がすべて記された標準的なスミスチャートは、初めて見るとあらゆる方向に線がごちゃごちゃ伸びてほとんど理解不能に見えるかもしれませんが（図4）、実は上記の単純化したグラフをより詳細に描いたものに過ぎません。オンラインのDigiKeyイノベーションハンドブックにあるリソースから、スミスチャートの印刷可能版をダウンロードできます。

図4：典型的なスミスチャートは、ものものしく見えるかもしれませんが、上記の単純化したグラフをより詳細に描いたものに過ぎません。（画像提供：DigiKey）

スミスチャートは、設計上の多くの問題に対する唯一の解決策以上のもの、すなわち考えられる多数の解決策を示します。そのため設計者は、インピーダンス整合したインダクタとコンデンサの実際の値など、特定の状況に適した部品の値の組み合わせが、どの解決策で得られるかを判断できます。ほとんどの場合、このグラフの数値メモリは50Ωシステムに「標準化」されていますが、それはこの値がRF設計において最も一般的なインピーダンスであるためです。

スミスチャートはきわめて重要で役に立つため、ベクトルネットワークアナライザ（VNA）など、RFおよびマイクロ波アプリケーション向けの多くのテスト計測器は、スミスチャートを作成して表示できます。たとえば、Teledyne LeCroyのVNAであるT3VNAは、そのようなモードを備えています（図5）。

図5：ベクトルネットワークアナライザT3VNAは、取得したデータをスミスチャート形式で表示できます。（画像提供：Teledyne LeCroy）

スミスチャートの使用法を習得する難易度は？このような質問のほとんどに言えますが、いろいろな学生に微積分学や電磁場理論の難しさをどう感じるか尋ねるのと同じです。つまり人によります。ネット上には、スミスチャートの基礎から始めて、さらに伝送路の方程式や解析的な見方を説明したテキストや動画がたくさんあります。それらは、スミスチャートを使用する多数の例も扱っています。もちろん、スミスチャートの作成、スミスチャートを使用した問題の構成、選択肢の評価などを容易にしてくれるアプリやプログラムもあります。ただし、それらに頼る前に、まずはスミスチャートの基礎を理解することが大切です。

まとめ

80年以上前に開発され、私たちが知っているRF設計が行われるずっと前から存在しているグラフが、今でも紙の図面やソフトウェアを使うRF設計の課題を解決する上で重要なツールのひとつであるのは驚くべきことです。どちらの場合に使うにせよ、スミスチャートはRFパラメータを表示および評価し、設計の代替案や関連するトレードオフに対する洞察を得るための強力なツールです。スミスチャートの威力とそれがどう役に立つのかを知る最善の方法は、実際にそれを使い、公開されている多くの例のいずれかに取り組んでみることです。

お勧めの記事

1 – 「スミスチャート：今もRF設計に欠かせない“古来の”グラフ」

https://www.digikey.jp/ja/articles/the-smith-chart-an-ancient-graphical-tool-still-vital-in-rf-design

2 - 「SAWフィルタが非実用的な個別素子実装からワイヤレス製品を救う」

https://www.digikey.jp/ja/articles/saw-filters-rescue-wireless-products-from-impractical-discrete-implementations

3 – 「ワイヤレス設計における低ノイズおよびパワーアンプの基礎を理解する」

https://www.digikey.jp/ja/articles/understanding-the-basics-of-low-noise-and-power-amplifiers-in-wireless-designs

4 – 「ログアンプの使用によるワイドダイナミックレンジRFおよび光リンクの感度および性能の向上」

https://www.digikey.jp/ja/articles/use-log-amps-to-enhance-sensitivity-logarithmic-amplifiers