オシロスコープを使って周波数応答を迅速かつ簡単に測定する方法

フィルタでは周波数応答を確認する必要があります。あるいは、アンプの帯域幅を測定しますか？周波数応答アナライザやネットワークアナライザの上でマウスの左ボタンを押したままカーソルをドラッグする必要はありません。測定は、オシロスコープと高速エッジ（fast edge）の矩形波を使って行うことができます。

周波数応答の測定には、測定の周波数範囲にわたって一定の振幅を持つ入力が必要です。周波数スペクトルが平たんな信号には、掃引正弦波、インパルス、広帯域ノイズの3種類があります。この3つのうち、インパルス応答は最も早く結果が出ます。では、インパルス波形を得るにはどうしたらいいのでしょうか？

回路解析の基本を思い出してください。インパルスはステップ関数の微分です。テストするデバイスのステップ応答があれば、それを微分することでインパルス応答に変換することができます。ほとんどのベンチトップオシロスコープには、数学関数パッケージの一部として積分と微分が含まれています。この例では、Teledyne LeCroyの500メガヘルツ（MHz）オシロスコープHDO 4054Aが使用されています。オシロスコープの帯域幅は、系統的振幅誤差を0.5デシベル（dB）未満に抑えるために、測定するデバイスの帯域幅の5倍を超える必要があります。別のオシロスコープとしては、Teledyne LeCroyのWAVESURFER-3054Zがあります。

ステップ関数を得るにはどうすれば良いでしょうか。その手順は簡単です。矩形波やパルスの立ち上がりエッジと立ち下がりエッジを分離するとステップ関数になるからです。ステップ関数を微分すると、インパルスになります。これは、図1で、10キロヘルツ（kHz）の矩形波の立ち上がりエッジを例として示されています（一番上のトレース）。

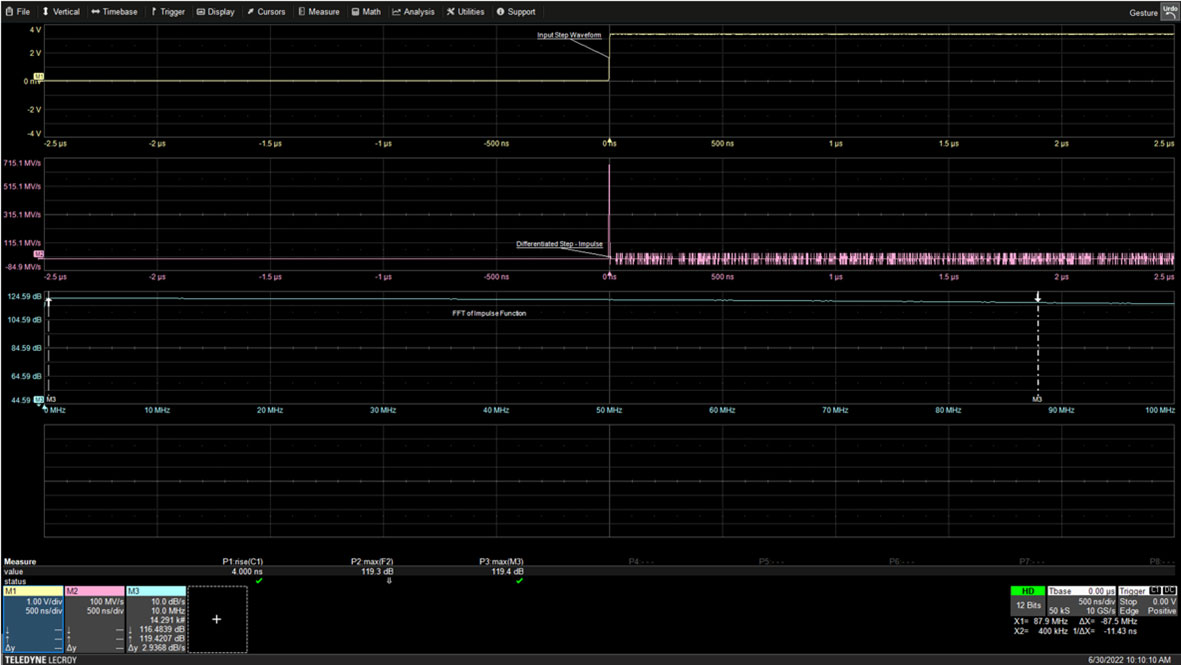図1：10kHzの矩形波の立ち上がりエッジは、微分するとインパルス関数になります。インパルスのスペクトルは平たんで、帯域幅が矩形波の立ち上がり時間に反比例しています。（画像提供：Art Pini）

このオシロスコープでは、当該のエッジが5マイクロ秒（ms）しか捕捉されていません。100msの矩形波のバランスがこの画面には表示されていません。ステップ関数は、オシロスコープの数学機能で微分され、中央のトレースとして表示されています。インパルスの高速フーリエ変換（FFT）は、一番下のトレースに示されています。インパルスの帯域幅は、矩形波の立ち上がり時間によって決まります。この場合、トレースグリッドの下にある測定パラメータP1の下に表示されているように、立ち上がり時間は4ナノ秒と測定されています。インパルスの帯域幅は、0.35を、単極振幅応答を持つオシロスコープの立ち上がり時間で除算した値として計算できます。

この例の結果は、FFTディスプレイの右側にあるカーソルが指し示す数学トレースM3の注釈で示される値（87.5MHz）となります。87.5MHzのFFTの振幅は、最大値119.43dBに対して116.48dBであり、最大値から約-3dBとなるので、これによって信号帯域幅を確認することができました。

周波数応答測定の対象となる信号源は、十分な測定帯域幅を確保できるような高速の矩形波またはパルス波である必要があります。図中の4nsエッジは、Teledyne LeCroyの150MHzの任意波形発生器T3AWG2152-Dで生成したものです。立ち上がり時間がはるかに高速な2nsの信号源としては、200MHz、2.4ギガ（G）サンプル/秒（Gサンプル/秒）の任意関数発生器であるTeledyne LeCroy製T3AFG200が挙げられます。2nsの立ち上がり時間により、175MHzの信号帯域幅が得られます。

デジタルローパスフィルタの周波数応答

次の例では、Teledyne LeCroyのHDO4054AオシロスコープとT3AWG2152-Dを用いて、デジタルローパスフィルタの周波数応答を測定しています（図2）。これらのフィルタ測定値は、各トレースの左側の列に表示されています。

フィルタ入力にはステップ信号が適用されます。フィルタ出力は微分されて表示されます。フィルタは帯域幅が限られているため、インパルス応答が広がっていることに注意してください。フィルタ出力はFFTにかけられ、平均化されて、フィルタの振幅周波数応答が生成されます。

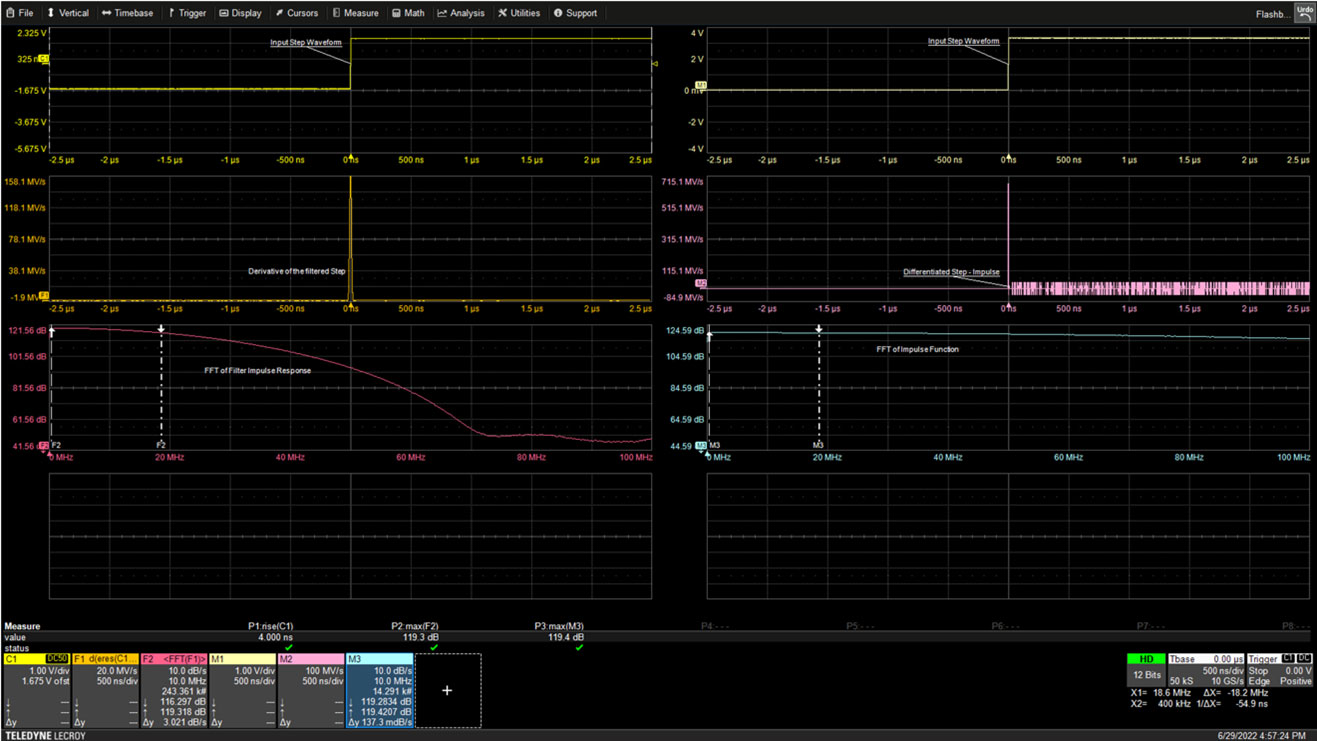図2：ステップ信号（左上のトレース）はフィルタ入力に適用されています。フィルタ出力は微分され、中央左のトレースに表示されています。フィルタリングされた信号に対するFFT（左下のトレース）は、フィルタの周波数応答を示しています。（画像提供：Art Pini）

図2の注釈では、フィルタ出力に対するFFT上のカーソル位置には、18.6MHzの周波数における帯域幅として-3dBが表示されています。これがフィルタ帯域幅です。同時に、右下のトレースのインパルス関数に対するFFTのカーソル位置が指し示すM3の注釈には、18.6MHz時に0.12dBだけ減衰したことが表示されており、信号源が概ね平たんであることがわかります。

まとめ

ご説明してきたように、周波数に依存する部品の応答は、高速エッジの矩形波に作用するオシロスコープの基本機能で迅速かつ簡単（ネットワークアナライザや周波数応答アナライザを使用する必要がない）に測定することができます。