ADCは単なる乱数発生器でいいのか？

A/Dコンバータ（ADC）の性能はどの程度でしょうか。この質問は、ADCが持つ分解能ビット数について尋ねているわけではありません。16ビットADCが常に16ビットの有効な情報を提供していない事実は、驚くべきかも知れません。「多くの16ビットADCは、実際には7ビットADCと9ビット乱数発生器として動作している」 と、Mike Stone氏は「Choosing an ADC（ADCの選択）」の中でこう述べています。この記事では、ADCが有効なデータよりも多くの乱数を生成しているかどうかを判断する方法と、そのランダム性を低減するいくつかの簡単な方法について説明します。

簡略化した設定を考えてみましょう。ADCがフォトレジスタの電圧を測定する場合です。図1の12ビットADC（V_FS = 3.3V）が2048の値を出力した場合、フォトレジスタの電圧は1.65Vということになるのでしょうか。

図1：フォトレジスタ電圧測定用の簡易ADCセットアップ。（画像提供：Nathan Jones氏）

いいえ、必ずしもそうとは限りません。実証のため、2回目のサンプル、そして3回目のサンプルを取得し、さらに実際に10万回のサンプルを取得して結果をプロットしてみましょう。その結果、ADC値の分布（図２）が確認できるはずです。設定値に変化がなければ、これらのいずれかがフォトレジスタの真の電圧であり、最も可能性が高いのは、これらの全サンプルの平均値となります。

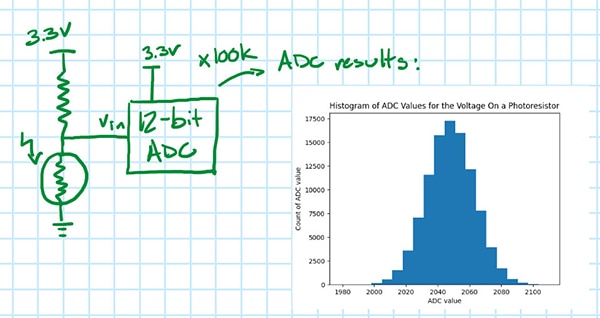図2：挿入図は、フォトレジスタ電圧の10万回のサンプル取得時におけるADC値のヒストグラムを示しています。（画像提供：Nathan Jones氏）

ここで別の疑問が生じます。このばらつきの一部は、入力信号自体の実際のばらつきである可能性はないでしょうか。はい、そう可能性はあります。これを検証するため、抵抗分圧器を既知のノイズレベルを持つ電圧リファレンス（図3）に交換し、再実験を行います。

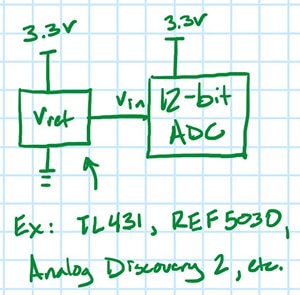図3：抵抗分圧器の代わりに電圧リファレンスを使用した新たな試験回路。（画像提供：Nathan Jones氏）

理想的には、使用する電圧リファレンスのノイズレベルは、ADCで予想されるノイズレベルの 1/3未満であるべきです（例えば、ADCが±1LSB（上記の例ではADCを使用すると±0.8 mVになる）と予想される場合、電圧リファレンスのノイズレベルは0.27ｍV_pp未満が理想的）。この条件を満たす場合、非相関ノイズは二乗和の平方根（式1）をとって合成されるという事実に基づいて、測定されるノイズのすべてがADCに起因すると考えられます。

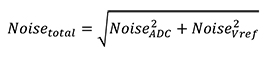[1]

Noise_Vref = Noise_ADC/3ならNoise_total = 1.054 × Noise_ADCとなります。これは、電圧リファレンスが総ノイズのわずか5.4%しかなく、無視できる量であることを意味します。もし電圧リファレンスのノイズがADCからのノイズの1/3よりも多いことが判明した場合、測定された標準偏差からその影響を差し引くことを忘れないでください（式2参照）。

[2]

電圧源のノイズレベルを把握する方法

最も簡単な方法は、データシートで確認することです。Texas InstrumentsのREF5030のデータシート例では、ノイズレベルが9μV_ppであることが示されています。

図4：出力電圧ノイズ仕様を示すREF5030のデータシートからの抜粋。（画像提供：Texas Instruments）

データシートにノイズレベルが記載されていない場合（または単にその値を確認する場合）、オシロスコープで測定してください。ただし、その前にオシロスコープのノイズフロアを把握しておく必要があります。この測定は、オシロスコープの入力端子の1つをグランドに接続し、表示される信号の変化の実効値（RMS）を測定することによって行うことができます。図5は、Analog Discovery 2（AD2）を用いてこの測定を行った結果を示しており、RMSノイズが約0.9mVであることを示しています。興味深いことに、この値は時間基準を8µs/div以上に増やすと（µVレンジまで）減少します。おそらく、AD2がオーバーサンプリングとデシメーションを使用して有効分解能を高めているためと考えられます。

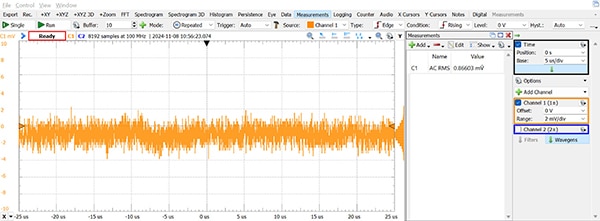図5：Analog Discovery 2オシロスコープのノイズフロアレベルプロット。（画像提供：Nathan Jones氏）

電圧源を測定する場合、オシロスコープ信号に生じる変化は、電圧源とオシロスコープ双方のノイズが合成された結果となります。これらのノイズ源が相関していない限り（実際には相間している）、測定ノイズは、Noise_measured = √(Noise²_Scope + Noise²_Vref)、Noise_Vref = √(Noise²_Measured - Noise²_Scope)となります。AD2で生成された2V_DC信号を測定した際、ノイズは1.2mVでした（図6）。

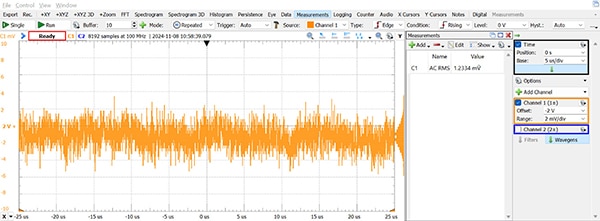図6：この2VDC信号のプロットは、オシロスコープのノイズが1.2mVであったことを示しています。（画像提供：Nathan Jones氏）

これは、AD2の信号発生器にも約0.9mVのノイズレベルが存在していることを示しています。このノイズレベルは、10ビットADCの試験には十分低い値です（0.9mVは、フルスケール3.3Vの読み出しの10ビットADCにおいてLSBのちょうど1/3弱に相当）。より高分解能のADCを使用する場合、このノイズは測定時に考慮する必要があります。

図7：挿入図は、電圧リファレンスを用いたフォトレジスタ電圧の10万回サンプルについて、ADC値の新しいヒストグラムを示しています。（画像提供：Nathan Jones氏）

これは非常に良好な結果です。2番目のヒストグラム（図7）ではX軸が2052までしか表示されていない点（このグラフ［図8］の分布は標準偏差1LSB）、一方最初のグラフでは2100まで表示されている（標準偏差は15LSB）点に注目してください。これはADCのDCヒストグラム試験と呼ばれ、標準偏差は事実上ADC内のノイズ量を効果的に示しています。ADCで値を測定するたびに、アナログピンの真の値がその値の±1標準偏差内に収まる確率は68%ですが、真の値がその値の±3標準偏差内に収まる確率は99.7%です。

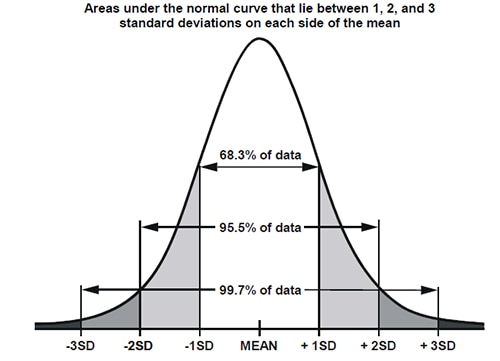図8：標準偏差を伴う分布曲線。（画像提供：https://i.sstatic.net/jkMDV.png）

この標準偏差をLSBからボルトに変換すると、ADC の入力換算ノイズになります（式 3）。

[3]

もしADCのノイズが非常に小さく、すべてのADCコードが単一のビンに本当に収まってしまうなら、ADC基準電圧を下げてみてください。ノイズレベルは変わりませんが、以前より多くのADCコードを占有するため、入力換算ノイズの適切な値を求めることが可能になります。

ADCの有効分解能およびノイズフリーコード分解能（NFCR）は、このノイズがADC分解能を制限する程度を表します。これらは、ADCコードの全範囲を、1（式4）または6.6標準偏差（式5）の幅のビンに分割することで算出されます。

[4]

[5]

本質的に、ADCの結果の最後の数ビットが間違っていたり、あるいはノイズの影響を受けている可能性が高くなるため、結果に含まれる実際のビットは少なくなります。

DCヒストグラム試験のもう少しわかりやすいバージョンでは、オシロスコープの場合と同様に、ADCの入力を単に接地し、ADCの結果のヒストグラム（図 9）を作成します。

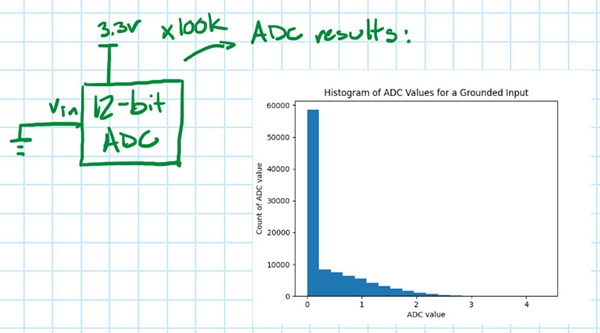図9：挿入図は、入力を接地した状態でのADC出力電圧サンプルのヒストグラムを示しています。（画像提供：Nathan Jones氏）

このヒストグラムの標準偏差もまた、ADCノイズの指標となります（ただし、0Vの読み取り値に影響しないADC基準電圧のノイズによる影響は除く）。しかし、この値は楽観的に低めに見積もられています。ADCはおそらく0V未満の値を0として出力するので、真のノイズ分布の半分しか確認できていないと考えられます。この場合、分布が平均値を中心に対称であると仮定し、分布が対称になるよう中央値を十分に負の数値に変更した上で、その標準偏差を計算することでADCノイズを近似できます（図10）。

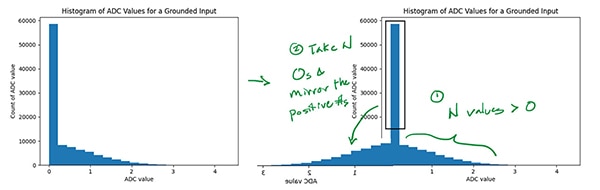図10：図9のヒストグラムを反転させてADCノイズを近似した図。（画像提供：Nathan Jones氏）

では、このノイズに対してどのような対策が可能でしょうか。ADCの分解能がプロジェクト要件を満たしている場合（幸運なことに）、ADC測定には常に次のような不確実性が伴うことを念頭に置いてください。

• 2つのADC値を比較する場合、互いが6.6σ以内であれば（比較結果に99.7%の信頼度）、あるいは互いに1σ以内であれば（比較結果に68%の信頼度）、同等とみなすようにしてください。
• ADC値を閾値と比較する際、（サーモスタットのように）ヒステリシスを閾値比較に追加し、ノイズのみによって組み込みシステムがその閾値の上下で再トリガされるのを防ぎます。

もしADCがプロジェクトの要件を満たさなくなった場合、その性能を改善するために試すことができる簡単な方法がいくつかあります。ハード面では、次のような対策が挙げられます。

• AVCCとAREF用に低ノイズのリファレンス電圧（Texas InstrumentsのREF5030またはEVVO TL431など）を使用する
• プリント回路基板（PCB）上でのアナログ信号とデジタル信号のクロストークを最小限に抑える
• ADC変換中にCPUを停止にして（MCUが対応している場合）、デジタルノイズを低減する

ソフトウェア側では、入力信号をオーバーサンプリング（つまり、N個のサンプルの平均を取る）することでノイズを低減できますが、これにより最大サンプリングレートが明らかに低下します。（実際、「オーバーサンプリングとデシメーション」と呼ばれる手法を用いれば、入力信号のオーバーサンプリング回数に応じてADCの分解能を向上させることができます。）

初期設定におけるDCヒストグラム試験の標準偏差が1LSBであると仮定します。ADCが2048を読み取った場合、今や真の値が1.650±0.008Vである可能性（68%の確率）はあるのでしょうか（図11）。

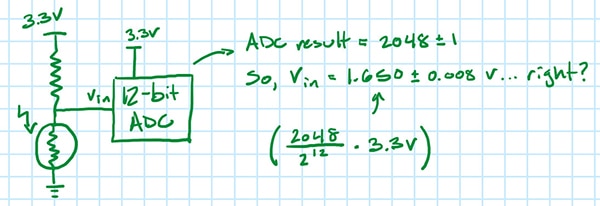図 11：図1の設定における標準偏差が1LSB、ADC出力が2048である場合、真の入力電圧は1.650±0.008Vとなるのでしょうか。（画像提供：Nathan Jones氏）

近いですが、残念ながら違います。これは、すべてのADCが特定の周波数で急激に変化する入力信号の測定に苦戦し、不正確な測定値（すなわちノイズ）が生じるためです。驚くべきことに、この現象が発生する周波数は、ADCの最大サンプリングレートをはるかに下回る可能性があります。つまり、サンプリングレート1MSPS（メガサンプル/秒）の12ビットADCであっても、入力信号が500kHz付近の場合、12ビットの分解能を実際には持たない可能性があります。また、入力信号の周波数が高い場合、そのADCの分解能は6ビット以下に低下する可能性があります。フォトレジスタ上の10Hzを超える信号を測定しようとする場合、ADCは実際には12ビットの分解能を持たない可能性があります。

ADCの分解能がより高い入力周波数でどの程度維持されるかを判断するには、既知の正常な信号（今回は正弦波）を入力し、ADC値がその既知の正常な信号とどの程度一致するかを測定します（図12）。（正弦波は「十分か」という点については、試験手順を明らかにした後に説明します。その方がより理解が深まるでしょう。）

図12：既知の正常な正弦波入力を用いた試験設定。（画像提供：Nathan Jones氏）

正弦波の生成には、ファンクションジェネレータ（多くのUSBオシロスコープに搭載されているものなど）、DDSチップ（Analog DevicesのAD9834など）、あるいはカスタムの正弦波発生器（たとえばウィーンブリッジ発振器を基に、Analog DevicesのMAX7400を用いて矩形波をローパスフィルタで処理するなど）が利用できます。本試験では、入力周波数がサンプリング周波数の整数倍でない値のみを使用することが極めて重要です（例えば、サンプルレートが100kHzの場合、入力周波数として1kHzは使用しないでください）。これは、正弦波が毎周期同じ位置で誤ってサンプリングされることを防止するためです。さらに、ADCに最大限の負荷をかけるためには、入力正弦波の振幅を、出力が「クリップ」しない最大の値に設定してください（例えば、上記の例におけるADCの場合、1.65Vよりわずかに小さい値など）。

ADCの結果を収集した後、データを正弦波にフィットさせて残留誤差を算出します。正弦波フィットはほぼ任意のデータ量でも実行可能ですが、最良の結果を得るためには、入力正弦波の完全な全周期が少なくとも5周期分は必要です。正弦波フィッティングアルゴリズムは、振幅、周波数、位相シフト、オフセットの初期推測値を指定して初期化する必要があるかもしれません（図13）。

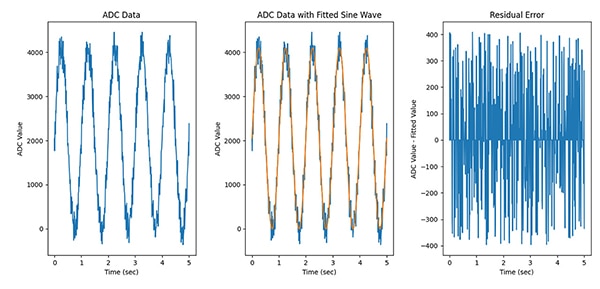図13：正弦波フィッティングアルゴリズムを使用することで、残留誤差を特定することが可能です。（画像提供：Nathan Jones氏）

この試験はADCの正弦波適合試験と呼ばれ、残留誤差のRMS値は、その特定の入力周波数におけるADCのノイズレベルを測定する指標となります。低周波領域では、RMSノイズはDCヒストグラム試験から得られる入力換算ノイズと一致するはずですが、高周波領域では、前述の周波数依存ノイズ源の影響により、ほぼ確実に劣化します。

正弦波適合試験から得られたRMSノイズ値を用いて ADCの有効ビット数（ENOB）を算出できます（式6）。これは、唯一のノイズ源である量子化ノイズのRMS値がADCのノイズと同一である理想的なADCのビット数に相当します。

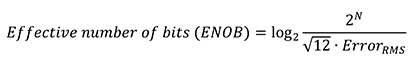[6]

この値は、使用された入力信号の周波数に固有のものです。ADCのより完全な特性を把握するためには、この試験を、対象とする最高入力信号周波数、あるいは最大サンプリングレートの半分までの全周波数で繰り返す必要があります。最大サンプリングレートの半分をはるかに下回る周波数でも、ノイズが大幅に増加することが確認される可能性があります（そしてENOBは大幅に低下します）。たとえば、STMicroelectronicsのSTM32F042K6に搭載されたADCに対して、まさにこの一連の試験を実施し、結果をプロットしました（図14）。

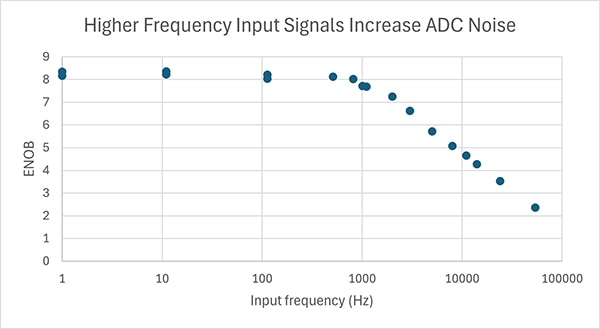図14：STM32F042K6マイクロコントローラに内蔵のADCの周波数ノイズ試験。（画像提供：Nathan Jones氏）

STM32F042K6マイクロコントローラのADCは1MHzでサンプリングが可能ですが、分解能は1kHzを超えると低下します。このADCで10kHzの信号を測定する場合、その時点で分解能は約5ビットしか得られないことになります。（なお、最大ENOBが約8.3である点にも留意してください。これは、DC時でも約10LSBのノイズが発生するためであり、ADCの有効分解能を最初から12ビットから約8.7ビットに低下させています。これらの試験は、未改造のSTMicroelectronicsのNucleo-F042開発ボード上で実施されました。前述の対策（「では、このノイズに対してどのような対策が可能でしょうか」）のいずれかを適用すれば、結果は大幅に改善されるでしょう。）

正弦波のノイズレベルを把握する方法

リファレンス電圧と同様に、正弦波のノイズレベルが事前に判明していない場合（つまり、データシートが入手できない場合）、オシロスコープを用いて測定する必要があります。前述の正弦波適合技術を用いることで、正弦波発生器からのノイズ特性を把握することが可能です。

1. まず、オシロスコープの入力端子をグランドに接続し、出力の実効値を算出することで、オシロスコープのノイズフロアを求めます（前述の「電圧源のノイズレベルを把握する方法」のセクションで説明した方法と同様です）。
2. 次に、正弦波発生器からの出力を測定し、その結果を完全な正弦波に適合します。その後適合結果と残留の実効値を算出します。その後、式2を使って正弦波発生器のノイズを算出します（この際。オシロスコープのノイズフロアをACノイズの近似値として使います）。

理想的には、正弦波のノイズレベルは、ADCから予想されるノイズレベルの1/3未満（つまり、正弦波が「スペクトル的に純粋」である状態）であることが望ましく、これにより測定ノイズへの影響は無視できるほど小さくなります。もし正弦波のノイズレベルがそれよりも高い場合は、残留誤差の実効値を算出して得られた測定ノイズから差し引くことを忘れないでください。

この試験は、ADCの試験に使用される予定のすべての入力周波数に対して繰り返す必要があります（正弦波発生器自体にも周波数依存性のノイズ源が存在する可能性があります）。

では、このノイズに対してどのような対策が可能でしょうか。まず、信号源とADCの間にローパスフィルタ（LPF）を入れることを推奨します。そのカットオフ周波数は、対象となる最高周波数の直上に設定し、高周波ノイズの抑制に役立てます（これは一般的に、あらゆるデータ収集システムにおいて「推奨される対策」です）。もし、対象の最高周波数信号が、ENOB対入力周波数のグラフで、最も高い周波数の信号が「ニー（knee）」点より低い場合、実際には分解能の低下は生じません。その 「ニー」点を越える信号を測定しようとする場合、より高周波数での分解能を改善するために試みるべきことがいくつかあります。具体的には次の通りです。

• アナログピンに接続されるデバイスの出力インピーダンスが非常に低いことを確認し、場合によってはバッファリングのためにオペアンプを挿入することも可能
• ADCクロックまたはそのサンプル/ホールド時間を可能な限り高速に調整し、内部コンデンサが十分に充電される時間を確保
• 低ジッタのADCクロックソースを使用し、システムを定期的にADCサンプリングを行うように設定

非常に狭い周波数帯域の信号が目的でない限り、次に行うべき最も単純明快な方法は、実際の入力信号がDCからLPFのカットオフ周波数まで等しい周波数成分を持つと仮定することです。したがって、ADC測定ごとのRMSノイズは、DCからカットオフ周波数までの正弦波適合試験で測定された平均RMSノイズとなります。先に述べたSTM32F042K6を使用して10kHzまでの広帯域信号を測定したい場合、ADC の各測定におけるENOBが約6ビット程度と想定して動作させるのが適切です。この値は、DCヒストグラム試験を用いて決定された値よりも十分低い可能性があり、より高い周波数成分が含まれている可能性がある場合には、ADC測定のそれぞれにおける確実性が低下することを示しています。

次に考慮すべき仮定は、センサとADCの間にLPFを追加し、DCからカットオフ周波数までのRMSノイズが±1LSBのみとなるようにすることです。ADCが2048を読み取った場合、今や真の値が1.650±0.008Vである可能性（68%の確率）はあるのでしょうか（図15）。

図15：回路にローパスフィルタを追加することで、真の値が1.650±0.008Vとなるのでしょうか。（画像提供：Nathan Jones氏）

おかしな話に聞こえますが、まだそうではありません。この記事ではADCのノイズを効果的に特徴づけましたが、その誤差についてはまだ説明していません。ここで示した試験を経ても、ADCの2つの値が同一か異なるかについてのみ確信が持てるのです。しかし、ADCコード2048が正確に1.65Vに対応するのか、それとも別の値に対応するのかは不明です。ゲイン誤差、オフセット誤差、および差動非直線性誤差（その他）の存在により、ADCコードから実際の電圧への変換は、 V_in=ADC result × V_FS/2^Nという単純な式では説明しきれない複雑さを伴う可能性があります。しかし、それはまた別の記事のテーマとします。

参考

1. Characterizing the Raspberry Pi Pico ADC（Raspberry Pi Pico ADCの特性評価）
2. Understanding Data Converters（データコンバータを理解する）（Texas Instruments）
3. Understand SINAD, ENOB, SNR, THD, THD + N, and SFDR so You Don't Get Lost in the Noise Floor（SINAD、ENOB、SNR、THD、THD + N、SFDRを理解し、ノイズフロアに惑わされないようにしましょう）（Analog Devices）
4. ADCの入力ノイズ：良いノイズと悪いノイズと厄介なノイズ、良いノイズとはノイズゼロのこと？（Analog Devices）
5. Getting the most out of the SAM D21's ADC（SAM D21のADCを最大限に活用する）（Thea Codes）
6. "Analog-to-Digital Converter Testing"（「アナログデジタルコンバータの試験」） （Kent Lundberg）
7. Dynamic Tests For A/D Converter Performance（A/Dコンバータ性能の動的試験）（Texas Instruments）
8. STM32マイクロコントローラで最高のADC精度を実現する方法（STM）
9. Enhancing ADC resolution by oversampling（オーバーサンプリングによるADC分解能の向上）（Atmel）
10. Fundamentals of Precision ADC Noise Analysis（高精度ADCノイズ解析の基礎）（Texas Instruments）
11. ARM® Cortex®-M0+ベースのMCUにおけるADCのゲイン/オフセット誤差の校正（Microchip）
12. Sine wave generation via low-pass filtering a square wave（矩形波のローパスフィルタによる正弦波生成）
13. Understanding the impact of digitizer noise on oscilloscope measurements（デジタイザノイズがオシロスコープ測定に与える影響の理解）（EETimes）
14. Understanding Effective Number of Bits（有効ビット数の理解）（Robust Circuit Design）