信号処理入門：移動平均フィルタ

信号とシステムは、電気工学において強力な概念です。これらは、情報が電気部品をどのように通過し、変化されるかをモデル化することができます。さらに、電圧などの信号がさまざまな電気部品によってどのような影響を受けるかを理解すれば、信号を自由に操作できる回路を設計することができます。したがって、抵抗器、コンデンサ、オペアンプ（OPアンプ）などの電気部品を組み合わせて、積分や微分などの数学的ツールをモデル化できることは、非常に興味深いことです。

たとえば、次の回路を見てみましょう（図1）。

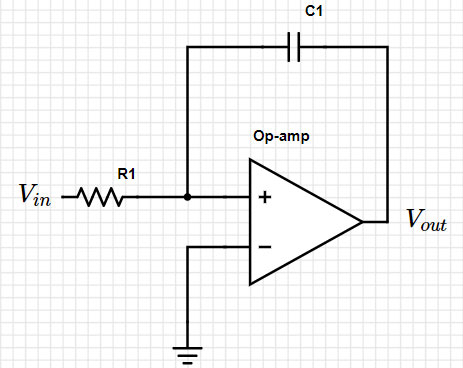図1：単純な積分回路。（画像提供：Mustahsin Zarif氏）

ラプラス領域に移ると、回路を次の式で表すことができます。

Vout = -(1/s)(1/RC) Vin

ラプラス領域の1/sは、実際には積分に相当します。したがって、OPアンプを使用した積分回路の回路モデルが得られました。しかし、現実の世界では、システムは常に何らかのランダムノイズに汚染されています。

積分回路は一旦保留して、より簡単な例として、図2のようにオシロスコープで入出力波形を測定できる電圧増幅回路を考えてみましょう。

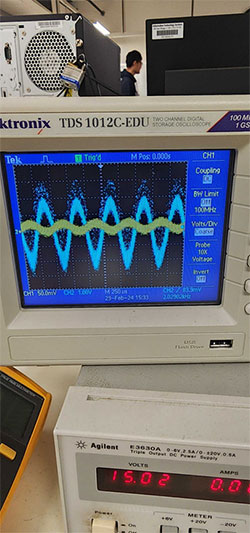図2：電圧増幅器の入出力波形。（画像提供：Mustahsin Zarif氏）

基本となる可視の正弦波形に追加されるランダムノイズは、ブレッドボード上に回路が作られているため、電気的な接続が不良であるなど、さまざまな要因に起因する可能性があります。このノイズは積分回路の波形も影響を及ぼし、このシリーズにおける今後のブログで信号処理のテーマとして取り上げます。しかし、私たちがしばしば関心を持つのは、いかにしてランダムな外乱を最小化する方法です。

フィルタリング技術

技術者は、これらの障害を克服するためにフィルタリング技術を採用します。フィルタリング技術は、1）有限インパルス応答（FIR）フィルタ、2）無限インパルス応答（IIR）フィルタに分類されます。

FIRフィルタは、出力は現在の入力値と直前の入力値のみに依存し、過去の出力値には依存しないため、この名前が付けられました。したがって、フィードバックのない非再帰的な構造を持ち、式1でモデル化できます。

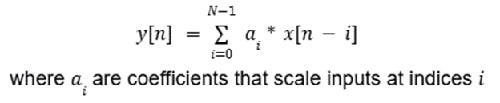式1：FIRフィルタの例式。（画像提供：Mustahsin Zarif氏）

積分回路は、出力が入力のみに依存するため、FIRフィルタの一例です。

一方、IIRフィルタは、任意の時点での出力が現在の入力だけでなく、過去の出力にも依存するため、フィードバックを有しています。これは式2でモデル化されます。

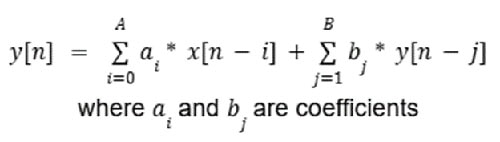式2：IIRフィルタの例式。（画像提供：Mustahsin Zarif氏）

図3はIIRフィルタのブロック図の視覚的表現で、入力と出力が遅延（z-i、z-j）、スケーリング（ai、bj）され、現在の出力を得るために加算される仕組みを示しています。これらの値を変更することで、さまざまな種類のフィルタを実装できます。

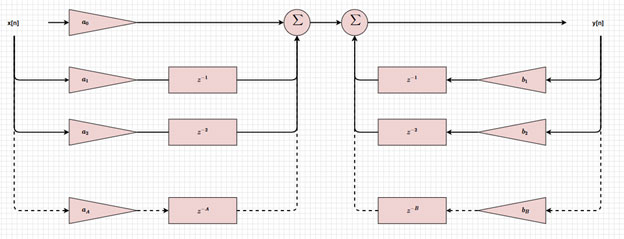図3：IIRフィルタのブロック図。（画像提供：Mustahsin Zarif氏）

フィードバックのないFIRフィルタのブロック図の場合、y[n]は最初の加算の結果のみとなります（図4）。

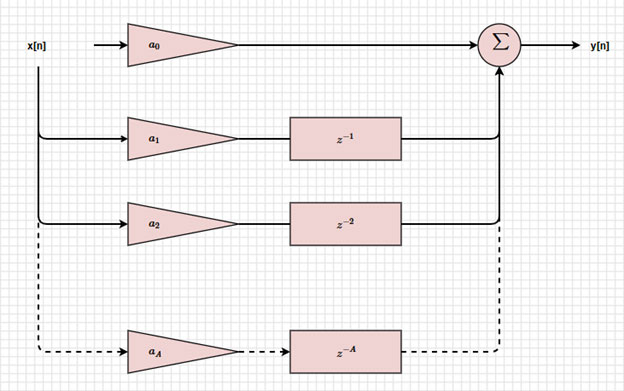図4：FIRフィルタのブロック図。（画像提供：Mustahsin Zarif氏）

さて、FIRフィルタとIIRフィルタの基礎を理解したところで、移動平均フィルタという例を用いて学んだことを説明しましよう。

移動平均は、現在の入力と一定数の過去の入力の平均を計算することで機能します（式3）。

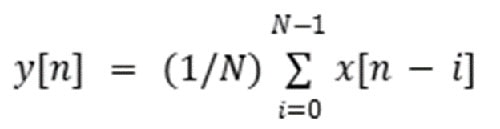式3：移動平均の式。（画像提供：Mustahsin Zarif氏）

ここで、N=ウィンドウサイズ/出力に寄与するサンプル数

この式から右辺にy項がないため、これがFIRフィルタであることがわかります。

しかし、式を再配置することで、IIRフィルタに変換できます。次のように考えてみてください。

N=5とすると、

y[5] = (x[5]+x[4]+x[3]+x[2]+x[1])/5、

およびy[6] = (x[6]+x[5]+x[4]+x[3]+x[2])/5

y[6]=(x[6]+y[5]-x[1])/5

したがって、現在の出力は前の出力に依存する（y[6]はy[5]に依存する）ことになります。

より一般的な表現では、以下のようになります。

y[n] = (y[n − 1] + x[n] − x[n − N - 1])/N

ここで、N=ウィンドウサイズ

このフィルタは、時間領域信号の平滑化に非常に効果的です。これは、ウィンドウサイズN = 11でpythonを使用してシミュレーションした図5に示す通りです。

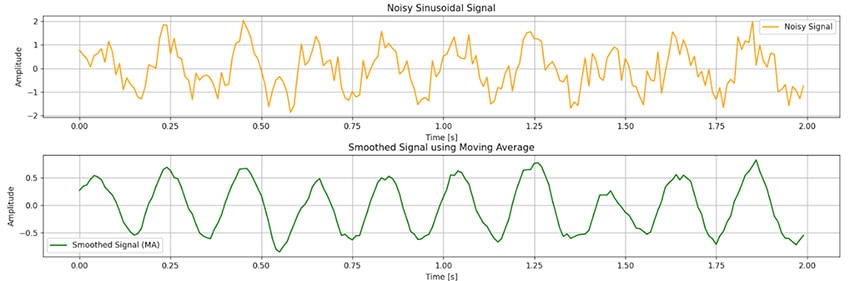図5：Pythonを使用した移動フィルタのシミュレーション。（画像提供：Mustahsin Zarif氏）

移動フィルタシミュレーションのPythonコードは以下の通りです。

コピーimport numpy as np

import matplotlib.pyplot as plt



# 正弦波のパラメータ

frequency = 5 # 単位：ヘルツ

sampling_rate = 100 # サンプリングレート（サンプル/秒）

duration = 2 # 単位：秒



# 時間軸の生成

t = np.linspace(0, duration, int(sampling_rate * duration), endpoint=False)



# クリーンな正弦波信号を生成

clean_signal = np.sin(2 np.pi frequency * t)



# 信号にランダムな白色（ガウス）ノイズを追加

noise_amplitude = 0.5

noisy_signal = clean_signal + noise_amplitude * np.random.normal(size=t.shape)



def moving_average(signal, window_size):

 window = np.ones(window_size) / window_size

 return np.convolve(signal, window, mode='same')



# ノイズ信号に移動平均を適用

window_size = 11

smoothed_signal_ma = moving_average(noisy_signal, window_size)



# ノイズ信号と平滑化信号をプロット

plt.figure(figsize=(12, 9))



plt.subplot(2, 1, 1)

plt.plot(t, noisy_signal, label='Noisy Signal', color='orange')

plt.title('Noisy Sinusoidal Signal')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.subplot(2, 1, 2)

plt.plot(t, smoothed_signal_ma, label='Smoothed Signal (MA)', color='green')

plt.title('Smoothed Signal using Moving Average')

plt.xlabel('Time [s]')

plt.ylabel('Amplitude')

plt.grid(True)

plt.legend()



plt.tight_layout()

plt.show()

まとめ

このブログでは、現実の世界でデータがノイズによって破損する仕組みを紹介しました。数式から期待する理想的な応答を得ることはできませんが、収集したデータから不要な特性をフィルタリングし、理想的な応答にできるだけ近づけることは可能です。これを行う方法は複数あり、その必要が生じるシナリオも多岐にわたります。このブログでは移動平均フィルタのシミュレーション応答で終わりましたが、次のブログでは指数移動平均フィルタがノイズの多い慣性測定ユニット（IMU）データを平滑化する方法を紹介します。